http://edelyn.livejournal.com/10823.html
пособие для кетайцев "Русский язык в картинках"

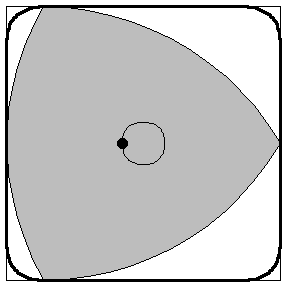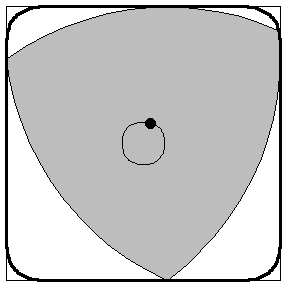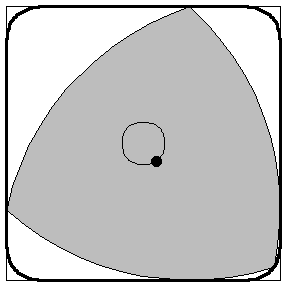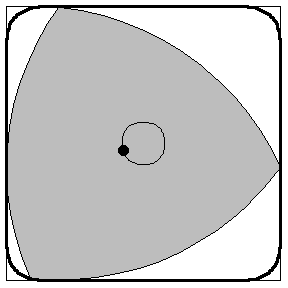
Бро́уновское движе́ние — тепловое движение микроскопических взвешенных частиц (броуновские частицы) твёрдого вещества (пылинки, крупинки взвеси, частички пыльцы растения и так далее), находящейся в жидкой или газообразной среде.
В математике, а точнее в теории случайных процессов, Броуновское движение (Винеровский процесс) - это гауссовский процесс с независимыми приращениями, у которого математическое ожидание равно нулю, а среднеквадратическое отклонение равно t*sigma.


Пусть подвыпивший матрос вышел поздно вечером из кабачка и направился вдоль улицы. Пройдя путь l до ближайшего фонаря, он отдохнул и пошел... либо дальше, до следующего фонаря, либо назад, к кабачку – ведь он не помнит, откуда пришел. Спрашивается, уйдет он когда-нибудь от кабачка, или так и будет бродить около него, то отдаляясь, то приближаясь к нему? (В другом варианте задачи говорится, что на обоих концах улицы, где кончаются фонари, находятся грязные канавы, и спрашивается, удастся ли матросу не свалиться в одну из них). Интуитивно кажется, что правилен второй ответ. Но он неверен: оказывается, матрос будет постепенно все более удаляться от нулевой точки, хотя и намного медленнее, чем если бы он шел только в одну сторону. Вот как это можно доказать.


Говорят, что в отсутствие ориентиров (солнце, звезды, шум шоссе или железной дороги и т.п.) человек бродит в лесу, по полю в буране или в густом тумане кругами, все время возвращаясь на прежнее место. На самом деле он ходит не кругами, а примерно так, как движутся молекулы или броуновские частицы. На прежнее место он вернуться может, но только случайно. А вот свой путь он пересекает много раз. Рассказывают также, что замерзших в пургу людей находили «в каком-нибудь километре» от ближайшего жилья или дороги, однако на самом деле у человека не было никаких шансов пройти этот километр, и вот почему.

Подробнее:
http://ru.wikipedia.org/wiki/%D0%91%D.. ..2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5

Лавэ наркомафии
http://www.webpark.ru/comments.php?id=21335

Решаем вместе!

http://www.hermes.net.au/bayling/repair.html
как избавиться от желтизны на старых линзах :)

Фишки для девелоперов:
http://www.usatt.org/rseguine/sw_dev/

Альтернативная история рок-музыки :)
http://gardenerm.livejournal.com/408921.html

Среди африканских слонов популярна шутка: они схлопываются в сингулярность, в нематериальную безразмерную точку, подкрадываются так к нерадивым туристам, и опять принимют свое нормальное трёхмерное состояние, что чревато резкой ударной волной потревоженного воздуха и гарантированным расслаблением сфинкера, причем как у туриста так и у слона.

Занятное чтиво - "Вообразим будущее Google"

http://www.webplanet.ru/news/reading-.. ..2/20/imagining_the_google_future.html
много букв!

как просверлить квадратное отверстие
http://mathworld.wolfram.com/ReuleauxTriangle.html

http://drugoi.livejournal.com/2109165.html#cutid1

черная дыра

Пхотошоп ?
У кого линейка с малатком под рукой - проверьте ? %)

В туркменских школах запретили проводить занятия по вождению после занятий по сексуальному воспитанию.
Потому-что ослик должен отдохнуть.

Некоторые мужчины, желая сдержать семяизвержение, думают о других мужчинах. Это самое опасное, что может быть. Потому что если вдруг кончишь, твоя жизнь изменится полностью. Это будет похлеще эксперимента академика Павлова.

http://www.myseminar.ru/index.php?m=view_text&id_text=5697
Хомоэволюция. Битва с дураками. (Без юмора. Чернушная реальность...)